VM2: Highly Efficient Conformational Searching
Implementation of Conformational Search
Basic VM2 algorithm
The mining minima approach is iterative, with successive searches for low energy minima and calculation of a cumulative free energy. Once no new lower energy minima can be found the cumulative free energy stops changing and the calculation is converged.
Conformational searching
The VM2 method requires reliable determination of the low energy minima in a system. For this a robust conformational search method that can drive the system over energy barriers is needed so the system does not get stuck in higher energy local minima. VeraChem has implemented two types of search, which can be used on their own or in combination, one, a rigid body translation/rotation search, and two, a mode distort-minimize search.
Rigid body translation/rotations
The search can sample systematically or randomly. The translation/rotation is broken into small steps. After each step a few energy minimization steps are carried out with respect to the non-ligand atoms in the system allowing relaxation in response to the ligand distortion. After each completed translation/rotation distortion a full quasi-Newton geometry optimization is carried out to produce a minimum.
Click the following image to see a movie of random translation/rotations distortions of a ligand in a protein binding pocket (no minimization).
Mode distort-minimze search
Molecular torsional modes are calculated via diagonalization of matrix of energy 2nd-derivatives transformed into internal coordinates with all bond and angle rows and columns removed. As such, the modes are linear combinations of dihedral energy functions that include the full set of energy terms (valence, nonbonded, solvation). The system is then distorted along these modes. The distortion is broken up into small steps and atoms not involved in the mode allowed to relax at each step. After a complete distortion the whole system is energy minimized via a quasi-Newton geometry optimization.
The following illustrates the case of a small molecule mode-distortion and minimization.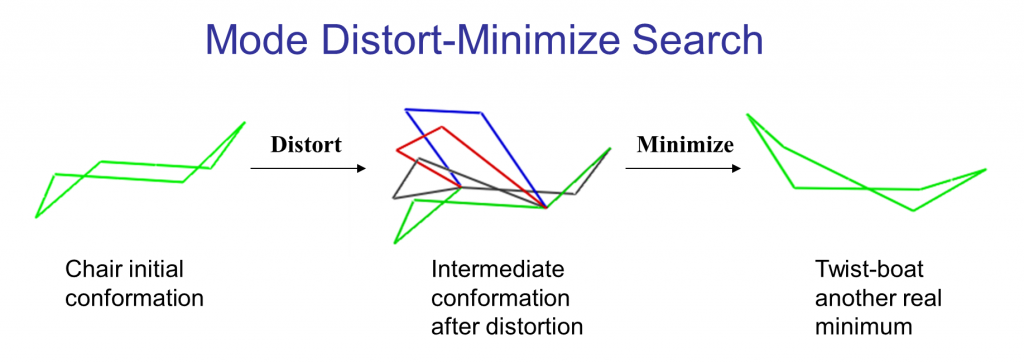
Each time a new lowest energy minimum is found it is subsequently used as a basis for the next mode distort-minimization. The number of torsional modes available depends on the size of the system.
The search can cycle through the available modes in order (low to high energy) or at random. In addition, a linear combination of randomly chosen pairs of these modes can be used to define the distortion.
To further illustrate this approach consider the following six-atom system and its internal coordinates.
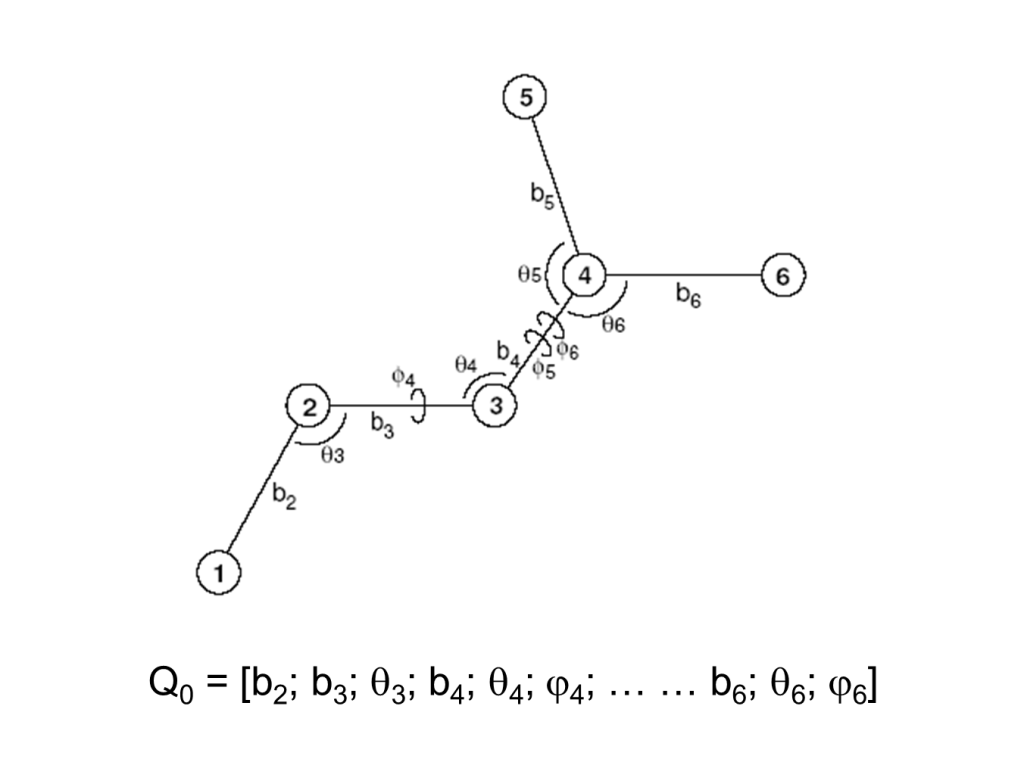The total energy 2nd-derivative (Hessian) matrix with respect to internal coordinates (bond, angle, torsion coordinates) can be calculated
The dimensionality of the Hessian is reduced by only allowing rows and columns with dihedral angles; furthermore, only one dihedral angle per central bond is retained
This reduced size Hessian is then diagonalized. The resulting eigenvectors are each a linear combination of the two dihedral “basis functions” and each represents a torsional mode distortion driver. The initial conformation can then be distorted along each driver D with step size α
and as previously described a quasi-Newton geometry optimzation carried out after the distortion is complete.
The following movies depict various types of mode distortions.
Random-pair mode distortions.
Ligand focused mode distortions.
Protein focused mode distortions.
Cycles of distort-minimize that use the previous lowest energy minimum as a basis for the next distortion provide a mechanism for efficient conformational searching to find the lowest energy minima of the system.
